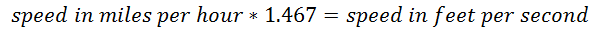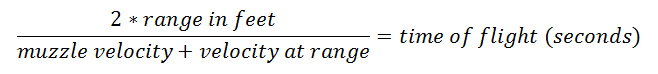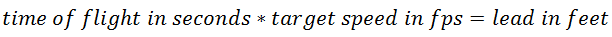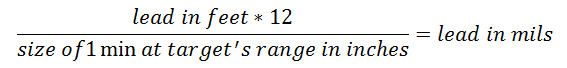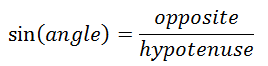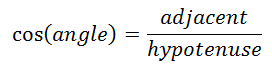Moving target - 3

The moving shooter is a problem I have never seen discussed anywere. Military snipers might face that situation. Police snipers, hopefully not! Hunters? Never, it is illegal to fire a firearm from a vehicule (in Canada anyway!).

The best solution (and the one that should always be used unless impossible), is to dismount and shoot from a static firing position.

But just for fun, lets do the math on that. Here the objective is to compensate for our motion.

---

1) the "simple" scenario

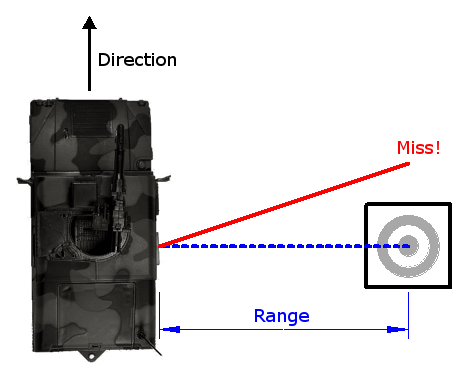
• The target is stationnary.
• The line of sight (in blue) is at a 90° angle to the direction of the vehicule.
• lets assume that the speed of the bullet in the direction of the vehicule - which is equal to the speed of the vehicule - remains contant throughout it's flight.

To calculate the lead, simply use the same method as in Moving - 1 and Moving - 2.

For this example, use this data:

• Range = 100 yards, or 300 feet.
• Vehicule speed = 30 mph.

Target speed

We need the speed in feet per second. We have it in miles per hour. So use this conversion formula:

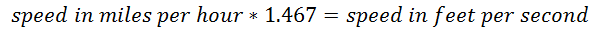
So in this example:

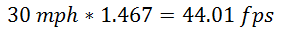
Time of flight

Remember this one?

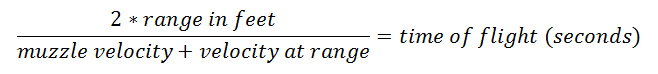
Here:

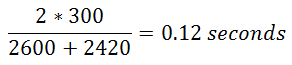
Lead

Using the lead formula:

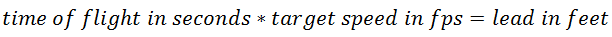
The lead will be:

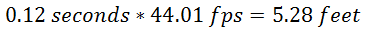
Convert this in mils:

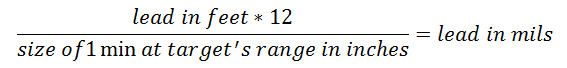
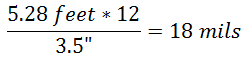
Well that is difficult! Unless you have a very special scope reticule, compensating for 18 mils is not feasible. It could be done by compensating with the internal scope adjusments AND mils in the reticule. But regardless, not an easy lead to apply. And remember to lead BEHIND the target (i.e. towards the back of the vehicule).

All this with a relatively slow vehicule and a very close target.

---

2) THE solution

The obvious solution is to stop. Not always feasible. Keep reading...

---

3) Shooting at an angle

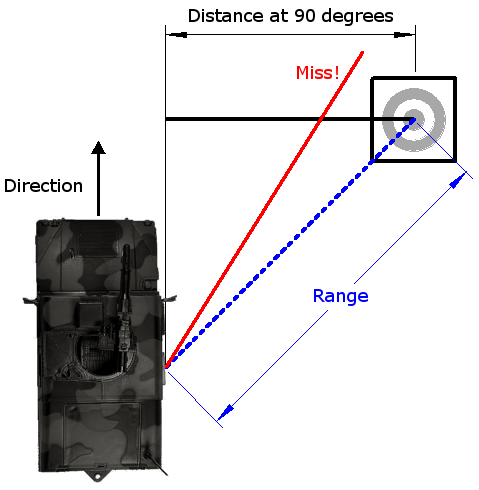
• The target is stationnary.
• The line of sight (in blue) is at an angle (green) to the direction of the vehicule.
• Again, lets assume that the speed of the bullet in the direction of the vehicule - which is equal to the speed of the vehicule - remains contant throughout it's flight.

For this exemple, use this data:

• Distance at 90° = 100 yards, or 300 feet.
• Vehicule speed = 30 mph.
• Angle = 45°.

Range

The range needs to be calculated. Trigonometry tells us that:

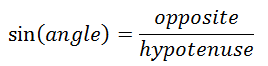
In our case, the opposite is the distance at 90° (100 yards), the angle is 45° and the hypotenuse is what we are looking for (the range).

Therefore:

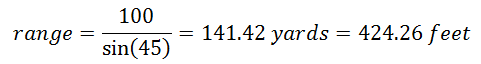
Target speed

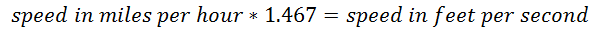
Here:

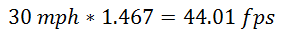
Time of flight

Now this is where it gets complicated. The bullet, when fired, is moving forward with the vehicule. This extra speed must be added to the muzzle velocity, and the velocity at range.

However, since the target is not directly in front of the vehicule, only a portion of the vehicule speed will affect the bullet velocity.

The speed vectors look like this (ref. The Velocity Vector and its Components):

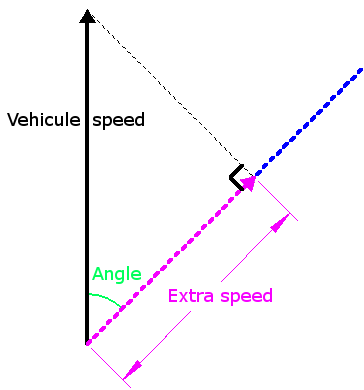
To calculate the extra speed, trigonometry is again used:

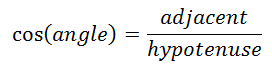
In our case, the adjacent is what we are looking for (the extra speed), the hypotenuse is the vehicule speed (44.01 fps) and the angle is 45.

Therefore:

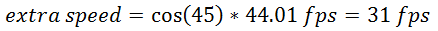
The time of flight formula can now be used:

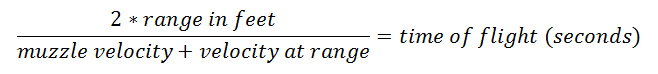
Here:

Lead

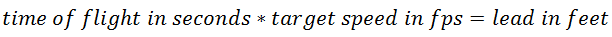
Here:

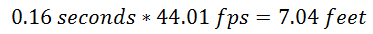
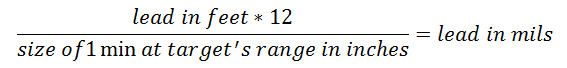
Finaly (!):

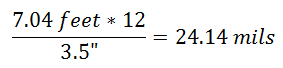
That does not really help, the compensation is even bigger than at 90°! This clearly demonstrates that a single shot while moving is not the best way to hit a target. Other weapons (machine guns or assault rifles) are more suitable to the task, since follow up shots are quick and the shooter can compensate between shots.

---

Final thoughts

Just "for fun" I calculated the angle that applying the lead generates. If aiming directly at the target produces a 45° angle, what angle results by shooting 7 feet behind it? The results are quite discouraging. I got 45.68°. Remember that 7 feet out of 300 is not a huge difference. And can anyone aim 0.68 of a degree?

This leaves the shooter with huge lead values. These can be attained by using a combination of both the scope internal windage compensation and a hold off using the mil reticule. But remember that you are moving at 30 miles an hour; you have very little time to calculate and apply compensation.

So this is one situation where the one shot rifle is clearly not the best option.

---

Formulas