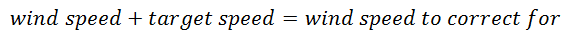Moving target - 2
We can now calculate a lead. From the previous page, we have:
- Target range.
- Target direction.
- Target speed.
- Bullet speed at the muzzle and at the target's range.
What is left to calculate is:
- Time of flight: how much time does it take the bullet to get to the target's range?
- Lead: what distance will the target travel during that time?
- Scope correction: how do you aim a lead?
And finaly:
- What about targets moving towards or away from you?
- Factoring in the wind.
1. Time of flight
As the bullet flies towards the target, it slows down. The speed varies due to drag. It is therefore not simple to calculate an exact time of flight.
The easiest method is to use ballistic software. However the following formula gives a close estimate:
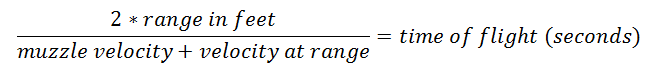
Example:
- bullet muzzle velocity: 2600 fps.
- range: 600 yards (or 1800 feet).
- bullet velocity at 600 yards: 1610 fps.
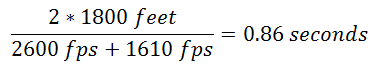
2. Lead
We now have everything we need to calculate a lead. We have a time of flight in seconds and the target speed in feet per seconds. The formula is:
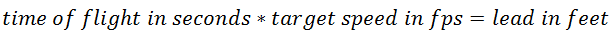
Example:
- time of flight: 0.86 seconds.
- target speed: 4.375 fps.
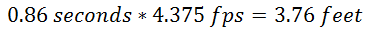
So aim 3.76 feet in front of the target and send it. By the time the bullet makes it to 600 yards, the target will have moved directly in it's path.
3. Scope correction
Hum... How can you aim 3.76 feet in front of a target!?! You have two choices here. Either you convert 3.76 feet to MOA and dial your scope for that value or you convert it to mils and use the dots in your scope to aim. I prefer the dots since the scope adjustments are already used for windage.
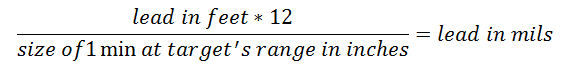
Example:
- lead: 3.76 feet.
- size of 1 mil at 600 yards: 21 inches.
- Target moving left to right.
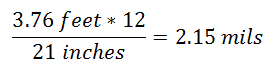
When the center of the target reaches 2.15 mils, send it. The target will continue moving up to the center the reticule, where your bullet will hit.
4. Targets moving towards or away from you.
Let's consider a target moving towards you, again at 4.375 fps, starting at 600 yards. The bullet takes 0.86 seconds to reach 600 yards, the target will have moved 3.76 feet. That is very close to 1 yard. Unless you are shooting at the Olympics or for some record, 1 yard out of 600 is not significant.
Obviously, the faster the target, the greater the effect. Calculate the effects for targets moving at 5, 10, 20, ... mph to see how much.
5. Factoring in the wind
Actually it is quite simple. Determine the wind speed as you normally would. Then apply this:
If the wind and the target are moving in the same direction:
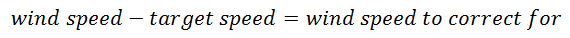
If the wind and the target are moving in opposite directions:
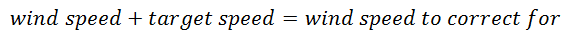
Formulas
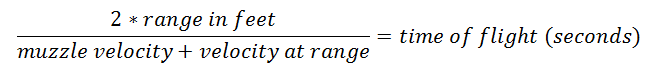
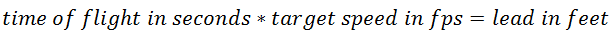
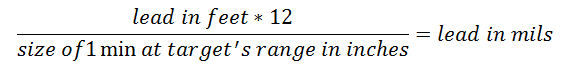
If the wind and the target are moving in the same direction:
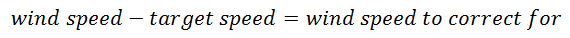
If the wind and the target are moving in opposite directions: